Pythagorean Theorem from “a new angle”

Pythagorean Theorem from “a new angle”

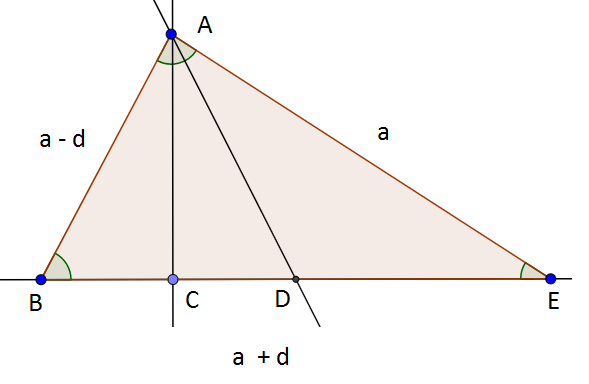Lets see the legacy theorem “The Pythagoras Theorem” from a totally new angle, I hope you understood (wink).

Proof-

Distance CD = (AB+AE)/10……………..(Piyush Theorem)10CD = (a-d) +a5CD + 5CD = 2a-d5(BD-BC) + 5(CE-DE) = 2a-d5BD – 5BC + 5CE – 5DE = 2a-d5CE – 5BC = 2a-d—– (BD=DE)5(CE-BC) = 2a-d————————eqn.1

Now,

CE^2 = AE^2 – AC^2BC^2 = AB^2 – AC^2CE^2- BC^2 = AE^2 – AB^2(CE+BC)(CE-BC) = (AE +AB) (AE – AB)(a +d)(CE – BC) = (a +a –d) (a-a +d)(a +d)(CE-BC) = (2a-d) dCE – BC = (2a-d) d/ (a +d) , put  value from eqn.15(2a –d) d/ (a +d) = (2a-d)5d/ (a +d) = 15d = a +d5d – d = aa = 4dIf it is a Right Angle Triangle,(a +d)^2 = a^2 + (a-d) ^2(a +d)^2 – (a-d) ^2 = a^2(a + d + a – d)(a + d –a +d) = a^2(2a)(2d) = a^2a = 4d QED.

 Copyrighted © Piyush Goel (1987)